Forecasting Buoy Observations Using Physics Informed Neural Networks and Numerical Models
Published Aug. 9, 2023
Ocean parameter forecasting is necessary for various tasks, like climate modeling, marine life population surveying, and water quality monitoring. There is a clear need in many industries to have fast and far-reaching forecasts. As such, the research and improvements in the ocean and climate modeling tools have continued to be interesting and necessary in literature. Some improvements stem from understanding that forecasting is an initial values problem, and by assimilating observation data, we achieve higher quality forecasts. However, observation data may be missing or not yet recorded to an extent that data may not be available. In this case, it may be desirable to forecast the sparse observations in a geographical region over a period in a generalized manner. In the case of the Physics Informed Neural Network (PINN), a model is trained using physics models as a form of regularization. Investigations into this type of modeling reveal suitable forecasts may be made in the case where data is sparse, due to intrinsically learning the partial differential equations (PDEs) during the training process.
This type of network is a recent addition to the deep learning community and is introduced formally in Physics-informed neural networks (PINNs) for fluid mechanics: A review. By providing initial and boundary conditions, PINNs are regularized with PDE outputs as they consider the underlying PDE instead fitting data points to unique solutions. Incorporating a loss function that encodes the governing physics equations by introducing PDE conditions is a novelty of PINNs. The result of these forecasting models is that we can incorporate noisy data into existing algorithms, ignore complex mesh generation, and tackle high-dimensional problems governed by parameterized PDEs. PINNs have also been investigated in industry informatics settings such as modeling crack propagation, modeling leakage, modeling faults, and modeling electric loads.
To test the ability of PINNs, we train recurrent neural network models which are regularized by HYCOM and ERA5 ocean and climatology models for the purpose of forecasting free floating ocean buoys. Therefore, initial experiments have focused on one generalized model which can forecast one geographical region at a time for a particular period. To achieve this, we combine buoy observations with numerical models to train surrogate deep learning models for more stable forecasting than with either feature alone. The regularization hyperparameter determines the ratio of observational and modeled data to be used in training the deep learning surrogate model, and we conduct a grid search to find which ratio was most performant. The Figure below demonstrates some initial results for forecasting buoy parameters over 24-hour increments using three different recurrent neural network models.
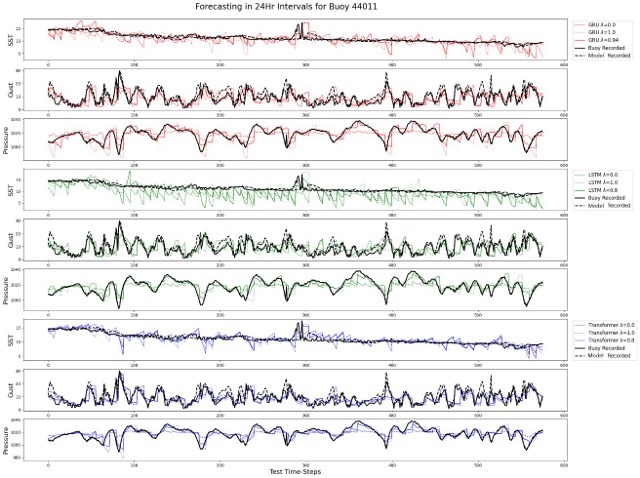
Overall, the regularization of neural networks using numerical models improves the general forecast performance compared to the non-regularized models. Our experimental results demonstrate the ability of PINNs to enhance the performance of neural networks for parameters that can be modeled using numerical models and demonstrates the utility of machine learning models to combine various climate models and sensor observations to improve forecast performance. Our method is used in a narrow scope in this experiment but can be modified to any task where sensor and observational data are comparable and used for future prediction.
As mentioned, the ability to train a PINN in any capacity requires a specialized loss function during the training phase. Our method differs when compared to other PINN training methods, mainly for two reasons. The first is that we use the output of numerical models (i.e., HYCOM and ERA5) as input data which is used to regulate the PINN, instead of including a physics based PDE as part of the training process. The second reason is that we use a ratio to control whether the model is trained from the numerical model or the ground truth observational data.
Ongoing research aims to consider whether the regularization can be determined as the model is trained, instead of searching for the best ratio by hand. That is, we aim to optimize how much the model is learning from the observation versus the numerical model during the model training process. This should decrease fine-tuning time while keeping the generalized expression of the model at around the same quality. We hope to improve the model to output forecasts which are more accurate and exist over larger geographical regions as well.

